The Segments Shown Below Could Form A Triangle
The Segments Shown Below Could Form A Triangle - The segments shown below could form a triangle. These segments could potentially form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. Let's check if this condition is. A triangle cannot have a perimeter of length zero. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
These segments could potentially form a triangle. A triangle cannot have a perimeter of length zero. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. Let's check if this condition is. The segments shown below could form a triangle. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the.
These segments could potentially form a triangle. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. Let's check if this condition is. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. A triangle cannot have a perimeter of length zero. The segments shown below could form a triangle.
the segments shown below could form a triangle ac9 cb7 ba16
Let's check if this condition is. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. A triangle cannot have a perimeter of length zero. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side..
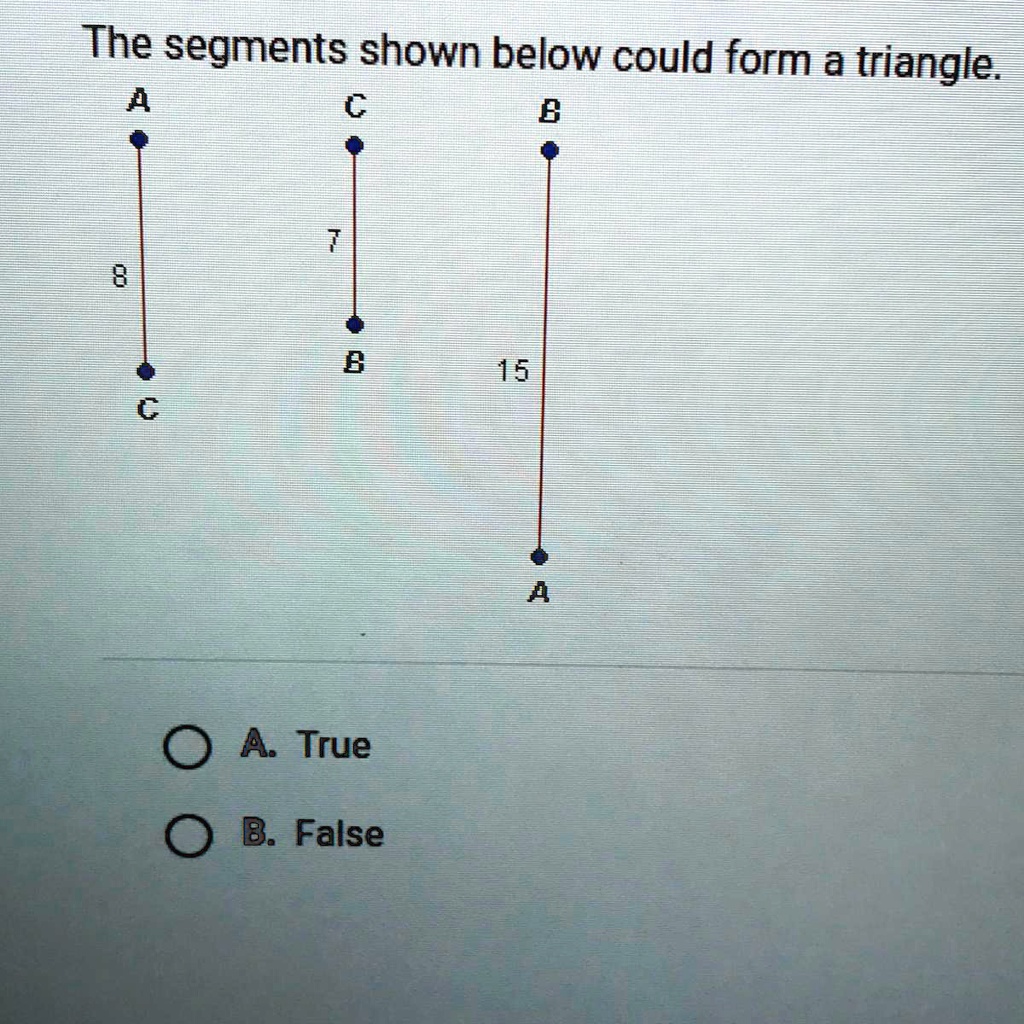
The segments shown below could form a triangle. OA. True OB. False
These segments could potentially form a triangle. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. A triangle cannot have a perimeter of length zero. Let's check if this condition is. The segments shown below could form a triangle.
The segments shown below could form a triangle. True or False
The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. Let's check if this condition is. The segments shown below could form a triangle. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. These.
The segments shown below could form a triangle.
For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. Let's check if this condition is. The segments shown below could form a triangle. The lengths.
The segments shown below could form a triangle. A. True B. False
Let's check if this condition is. These segments could potentially form a triangle. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. The segments shown below could form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any.
The segments shown below could form a triangle. А С B 5 6 В 12 O A
To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. The segments shown below could form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. The lengths given (ac=6, cb=5, ba=8) satisfy the.
The segments shown below could form a triangle. A с B 3 6 B C A O A
For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. The segments shown below could form a triangle. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. A triangle cannot have a perimeter of length zero..
SOLVED 'The segments shown below could form a triangle. The segments
The segments shown below could form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. Let's check if this condition is. The lengths.
The segments shown below could form a triangle. д C B 9 11 B C O A
For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. The segments shown below could form a triangle. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. A triangle cannot have a perimeter of length zero..
The segments shown below could form a triangle.True or False
For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. Let's check if this condition is. A triangle cannot have a perimeter of length zero. These segments.
For A Set Of Three Segments To Form A Triangle, The Sum Of The Lengths Of Any Two Sides Must Be.
A triangle cannot have a perimeter of length zero. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. The segments shown below could form a triangle. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the.
Let's Check If This Condition Is.
These segments could potentially form a triangle.